Preuves créatives avec des pigeons et des bo?tes
Un principe peut sembler simple, mais en mathématiques, il peut être une clé pour résoudre des problèmes exigeants. Le principe du pigeonnier est une bonne entrée en matière pour les élèves qui souhaitent découvrir les aspects créatifs de la preuve.
Parfois, les mathématiques ressemblent presque à du football. La résolution d'un problème épineux n'est alors pas une affaire solitaire, mais une ?uvre collective qui exige de la créativité et de la tactique. Les choses vont vite lorsque des élèves secondaires se réunissent pour résoudre des problèmes mathématiques à l'"ETH Math Youth Academy". Un élève lance une idée à la ronde, un deuxième prend la balle au bond, propose une solution, passe la balle à son coéquipier et celui-ci marque le coup : le problème est résolu.
Sur le plan du contenu, les sept élèves s'attaquent à une preuve : un samedi soir, il y a une fête en ville à laquelle participent plus de deux personnes. Comment démontrer qu'au moins deux participants ont exactement le même nombre d'amis ?
La solution se trouve dans ce que l'on appelle le principe du pigeonnier ou du tiroir, formulé pour la première fois en 1834 par le mathématicien allemand Peter Gustav Lejeune Dirichlet. Ce principe doit son nom au fait que l'on peut se le représenter de manière imagée à l'aide d'un pigeonnier.
Si l'on place quatre pigeons dans un colombier qui a trois cases, il doit y avoir au moins deux pigeons dans une case. Il en va de même si l'on répartit quatre perles dans trois tiroirs.
Le principe peut être généralisé : chaque fois que des objets sont attribués à certains ensembles et qu'il y a plus d'objets que d'ensembles, alors au moins un ensemble doit contenir plusieurs objets.
Le principe du pigeonnier a de vastes possibilités d'application : En tant que méthode de preuve, il s'est avéré aussi utile en géométrie qu'en théorie des nombres, en combinatoire, en théorie des graphes (théorie des réseaux), en logique formelle ou encore en informatique théorique.
La beauté des raisons supposées
"C'est la beauté des mathématiques : nous commen?ons par un principe simple et arrivons rapidement à des conclusions surprenantes et à des résultats inattendus", explique Kaloyan Slavov. Ce post-doctorant du Département de mathématiques fait de la recherche en géométrie algébrique et organise l'ETH Math Youth Academy.
L'ETH Math Youth Academy fait partie du programme de formation du P?le de recherche national "Mathématiques de la physique" (NCCR SwissMAP), qui encourage la recherche, l'enseignement et le transfert de savoir dans le domaine des mathématiques et de la physique théorique sous la direction de l'Université de Genève et de l'ETH Zurich.
Images de l'ETH Math Youth Academy
 Kaloyan Slavov transmet corps et ?me l'art de la démonstration originale.
Kaloyan Slavov transmet corps et ?me l'art de la démonstration originale.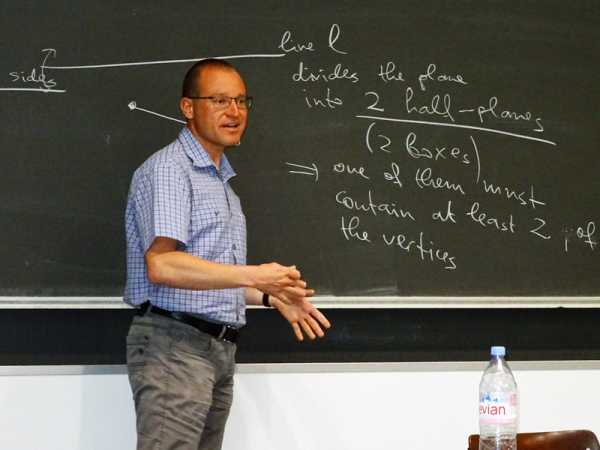 A l'aide d'un exemple tiré de la géométrie, les élèves secondaires s'exercent au principe du pigeonnier.
A l'aide d'un exemple tiré de la géométrie, les élèves secondaires s'exercent au principe du pigeonnier.
Preuves créatives ou qu'est-ce que la "colombe" ?
Pour les élèves secondaires aussi, le principe du pigeon devient rapidement plus exigeant. Ils doivent l'appliquer à un exemple de géométrie : une droite coupe un triangle, et ce de telle sorte qu'elle ne touche aucun sommet du triangle. Comment prouver, à l'aide du principe du pigeon, que la droite ne peut pas couper les trois c?tés du triangle ?
Dans cet énoncé, les élèves remarquent que la véritable difficulté du principe du pigeonnier est de trouver, au cas par cas, quels éléments peuvent être traités comme des "pigeons" et lesquels comme des "bo?tes". Il faut d'abord une idée lumineuse avant de pouvoir appliquer la méthode du pigeonnier à un problème donné.
C'est ce que Kaloyan Slavov veut faire comprendre aux élèves. En déterminant eux-mêmes ce qu'ils désignent comme colombes et comme bo?tes, ils apprennent à voir plus loin que le bout de leur nez pour trouver une solution et à utiliser les méthodes de preuve de manière créative. Cette capacité est utile dans les études et dans de nombreux domaines des mathématiques et de la vie quotidienne. Le Bulgare a lui-même étudié à Harvard, à Cambridge et au MIT.
Dans l'exemple de géométrie, la ligne droite divise le plan d'un triangle en deux demi-plans. Les points correspondent aux colombes et les demi-plans aux bo?tes, de sorte que l'un des demi-plans contient deux points et l'autre un seul. Le c?té du triangle qui relie deux sommets dans un demi-plan est alors celui qui n'est pas coupé par la ligne droite. Dans l'exemple de la fête, les participants à la fête correspondent aux colombes et le nombre d'amis aux bo?tes.
Les mathématiques, c'est plus que le calcul des chiffres
L'ETH Math Youth Academy initie aux approches mathématiques typiques. "Il suffit que les élèves s'engagent dans une pensée créative", explique Kaloyan Slavov, qui ajoute : "La créativité est le contraire de la routine." Ses cours se focalisent sur des problèmes qui ne peuvent pas être résolus par la routine, mais seulement si l'on part d'une idée créative, que l'on raisonne de manière subtile et logique et que l'on mène les preuves de manière strictement mathématique.
La récompense, explique Slavov, vient des mathématiques elles-mêmes : "Les gens se réjouissent lorsqu'ils reconnaissent l'ordre logique derrière les choses et voient que les raisons supposées sont effectivement vraies".
15 élèves participent aux cours pour débutants et avancés. Les le?ons de Kaloyan Slavov leur plaisent. Les cours sont passionnants, pas du tout "secs". On y apprend à démontrer et que les mathématiques sont plus que des calculs avec des chiffres. Ils sont surpris par la diversité des applications, des méthodes et des stratégies de résolution.
"Ce cours est cool", dit Yiqi du Realgymnasium R?mibühl. "Ici, il n'y a pas de solutions traditionnelles et le chemin vers la solution est créatif". Jonas, de Wetzikon, aime lui aussi le c?té créatif de la preuve : "Ici, on ne peut pas résoudre un problème avec un gabarit, mais on doit trouver une nouvelle solution à chaque fois".
